Tao Changes

Eleven years ago Terence Tao wrote an excellent short blog post about his perspective on one aspect of scheme theory. In the introduction, he enumerates four perspectives from which one can view a curve: he calls them 

• Algebraic geometry
• Commutative algebra
• Dual algebraic geometry
• Dual commutative algebra

Algebraic geometers often talk in all four of these perspectives at once, and implicit transitions from one to the other regularly happen several times a sentence. But each perspective gives us insight into the curve and what it "really is." Trying to keep up with these changes has made me feel like Tommy Flanagan trying to solo over the blazingly fast chord changes that underlie Coltrane's Giant Steps. These chord changes are now famous, and are called Coltrane Changes.

I call the fast changes in perspective that occur in so much of algebraic geometry Tao Changes...

—————————————————————

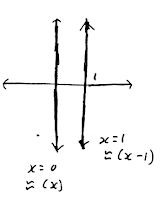
Draw two lines in the plane.

\(\operatorname{B}^{\operatorname{Maj}7}\): 

These are two parallel Euclidian lines. The space between them is undetermined, as we have not yet chosen a unit or imposed a coordinate system onto the blank plane. 

\(\operatorname{D}^{\operatorname{}7}\): 

These Euclidean lines are a set of points in the plane. We can make this description explicit by choose a coordinate grid, as Descartes did. Let's make one line the \(y\)-axis and the other the line \(x=1\). The lines are now just the set of points 

$$S = \{(a, b) \; | \; a \in \{0, 1\}, \; b \in \mathbb{R} \}.$$  

\(\operatorname{G}^{\operatorname{Maj}7}\): 

More than just a set of points, this object is an algebraic variety—the vanishing set of a polynomial. More broadly, in the context of polynomial functions on \(\mathbb{R}^2\), we can see each point \(p \in S\) as inducing an evaluation map, taking polynomials to their values on \(p\). Notice that \(x(x-1)\) is in the kernel of every one of these evaluation maps; thus \(S\) is nothing but the zero-locus of the polynomial \(f(x,y) = x(x-1)\). 

\(B\flat ^7\): 

But \(f\) is not the only polynomial in every kernel. In fact, if \(f\) and \(g\) are polynomials that vanish on \(S\), then so does \(f + g\); further, if \(h\) is an arbitrary polynomial, then \(hf\) also vanishes on \(S\) (where we have defined multiplication pointwise). Since the set of polynomial functions on \(\mathbb{R}^2\) forms a ring, denoted \(\mathbb{R}[x,y]\), this object is an ideal \(I\) of polynomials vanishing at \(S\) of this ring. (In fact, \(I = (x^2-x)\)).

\(E\flat ^{\operatorname{Maj}7}\): 

How about those polynomials which don't vanish on  \(S\)? How much can we learn about them? We can't distinguish any two polynomials which take the same value on this set. This implies that any two polynomials which differ by an element of \(I\) are indistinguishable. If we treat these two lines as a means of studying the behavior of polynomial functions, we conclude this object is a projection from \(\mathbb{R}[x,y]\) to quotient ring \(\mathbf{\mathbb{R}[x,y]/I}\).

\(\operatorname{Am}^{7}\):

Have we lost information in this process? How can we recover the fact that these are two different lines from the quotient ring (or from the projection to it)? Firstly, Hilbert's Nullstellensatz assures us that we can recover the points of the set by looking at the maximal ideals of  \(\mathbb{R}[x,y]/I\). Modern algebraic geometry broadens its focus from just the maximal ideals to all the prime ideals of this ring, which compose the "points" of an object called an affine scheme, denoted \(\operatorname{Spec} \mathbb{R}[x,y]/I\).  Commutative algebra tells us that \(\mathfrak{p}\) is prime (but not maximal) if and only if  \(\mathfrak{p}\) is the projection onto \(\mathbb{R}[x,y]/I\) of a prime (but not maximal) ideal of \(\mathbb{R}[x,y]\) which contains \(x^2-x\). Two ideals of \(\mathbb{R}[x,y]\) fulfill these hypotheses: \((x)\) and \((x-1)\). Indeed, these are the so-called "generic points" of the two lines. Some finicky commutative algebra verifies these are the only points. We have not lost any information: the quotient ring contains the fact that this object has two components, and that these components are lines.

\(\operatorname{D}^{7}\): 

These two generic points correspond to two subschemes—essentially subvarieties— \(\operatorname{Spec} \mathbb{R}[x,y]/I\), namely \(\operatorname{Spec} \mathbb{R}[x,y]/(x)\) and \(\operatorname{Spec} \mathbb{R}[x,y]/(x-1)\). These have maximal ideals corresponding to the sets 

$$S_1 = \{ (0,b) \; | \; b \in \mathbb{R}\} \;\;\;\;\;\;\;\; \text{and}  \;\;\;\;\;\;\;\; S_2 = \{ (1,b) \; | \; b \in \mathbb{R}\}$$

whose union is \(S\).

\(\operatorname{G}^{\operatorname{Maj}7}\): 

These two sets are lines, and a line is a one-dimensional object; in particular, they are the same "object" as the one-dimensional real-number line. In the language of algebraic geometry, these schemes are isomorphic the affine line: \(\mathbb{R}[x,y]/(x) \cong \mathbb{R}[y]\), and \(\mathbb{R}[x,y]/(x-1) \cong \mathbb{R}[y]\). These isomorphisms are via the evaluation map at \(x=0\) and \(x=1\), respectively. Like in so many cases in algebraic geometry, these evaluation maps are only good for one thing: telling us if polynomials vanish or not. Thus this object is nothing but a way to evaluate polynomials on one of the two lines via their general points.

\(B\flat ^7\): 

One of the mantras of algebraic geometry is that Vanishing Is Containment. If a polynomial vanishes on a line, its zero-locus contains that line, and a polynomial vanishes on a line only if it vanishes on the general point of that line. Thus the point of these morphisms is they can tell you if a curve contains either of these lines. For example, the curve defined by the zero-locus of \(xy-x^3\) maps to the zero polynomial under the first isomorphism, but not under the second—thus the curve contains the first (but not the second), line. 

\(E\flat ^{\operatorname{Maj}7}\): 

In Euclidian geometry,  angles, relative distances, and coincidence of lines are all inherent to the geometric objects we study. But in the projective world these qualities are irrelevant to the geometry at play. By homogenizing the ideal \(I\) with a new variable \(Z\), we obtain a new ideal \(J = (X^2-XZ)\), which vanishes on a set of lines in \(\mathbb{R}^3\), and since \(J\) is composed of homogenous polynomials, we can convert this into a figure in the projective plane. This setting is just as natural as the Euclidean one, and again, they are two lines.

\(F\sharp^7\): 

Projective objects have scheme-theoretic representations too; and just like in the affine case, in some sense the object which best represents the geometry is the set of polynomial functions on the space. In this case, the algebraic object we consider is the set of homogeneous polynomials in three variables modulo their value on the curve \(X^2=XZ\). The full object is denoted \(\operatorname{Proj} \mathbb{R}[X,Y,Z]/(X^2-XZ)\), and comes with function, a topology, traditional points as we expect.

\(\operatorname{B}^{\operatorname{Maj}7}\):

The same algebra-geometry correspondence which operates in the Euclidean (usually called affine) case operates here as well. By studying the the set of near-maximal ideals (in a technical sense), we can obtain the set of projective points which make up this variety. But, perhaps more fundamentally, just as in the affine case, studying the non-closed points—the prime ideals—reveals that this complex object is made up of... 

Two lines.